Lesson 2: Comparing and Reducing Fractions
/en/fractions/introduction-to-fractions/content/
Comparison fractions
In Introduction to Fractions, we learned that fractions are a manner of showing part of something. Fractions are useful, since they allow united states tell exactly how much we have of something. Some fractions are larger than others. For example, which is larger: 6/8 of a pizza or 7/8 of a pizza?
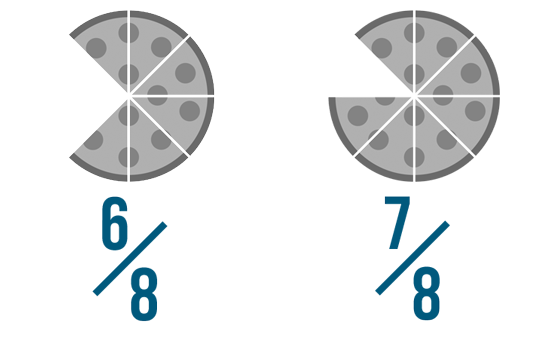
In this prototype, nosotros tin run into that 7/8 is larger. The illustration makes it easy to compare these fractions. Merely how could nosotros have washed it without the pictures?
Click through the slideshow to learn how to compare fractions.
-
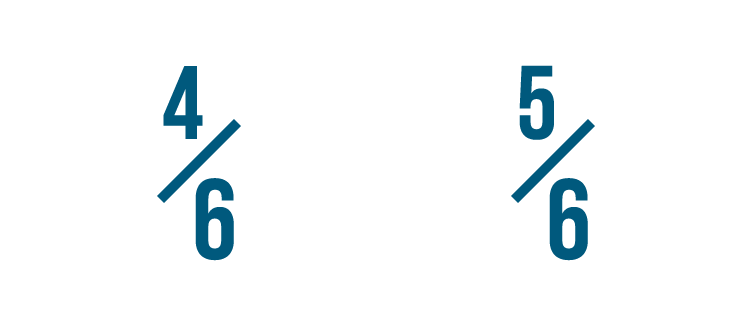
Before, nosotros saw that fractions take two parts.
-
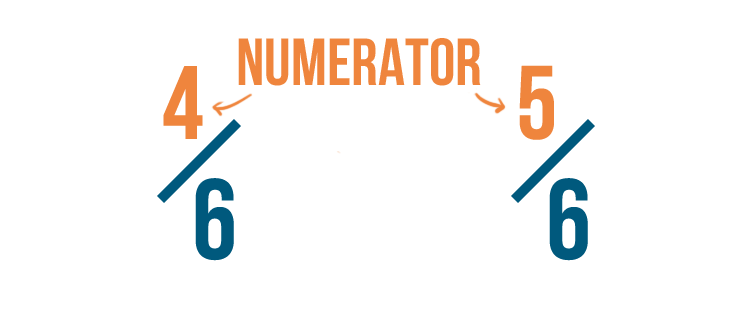
I part is the top number, or numerator .
-

The other is the bottom number, or denominator .
-

The denominator tells us how many parts are in a whole.
-

The numerator tells us how many of those parts we have.
-

When fractions have the same denominator, it ways they're dissever into the same number of parts.
-

This means we can compare these fractions just by looking at the numerator.
-

Hither, 5 is more than than iv...
-

Here, five is more than 4...so we tin tell that 5/half-dozen is more four/half dozen.
-
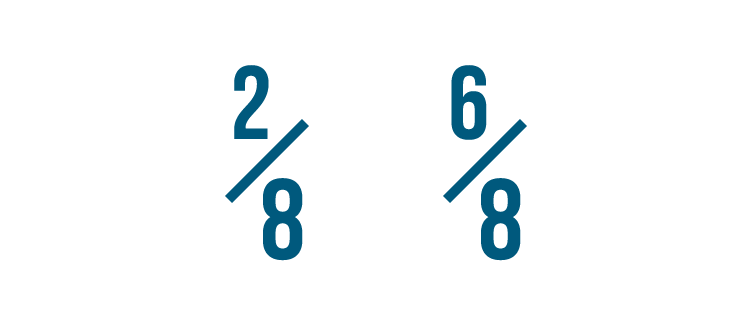
Let'southward expect at another example. Which of these is larger: 2/8 or half-dozen/viii?
-
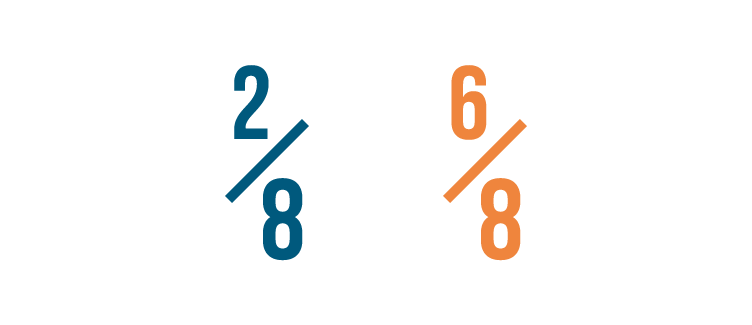
If you idea six/8 was larger, you lot were right!
-
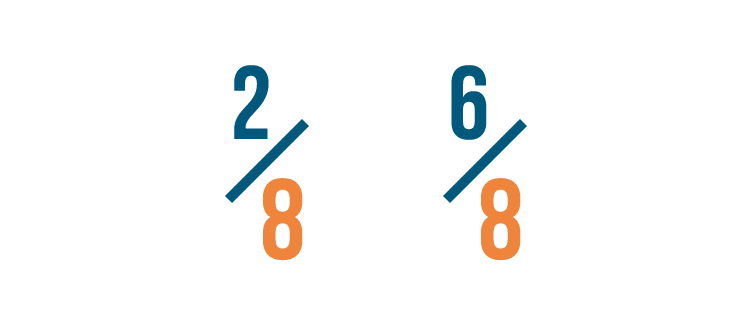
Both fractions accept the same denominator.
-
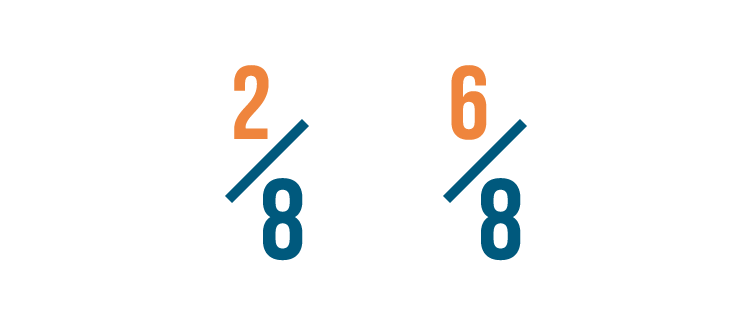
So we compared the numerators. 6 is larger than 2, so half dozen/8 is more than 2/8.
-

Every bit you saw, if two or more fractions have the same denominator, you can compare them by looking at their numerators. As yous can encounter beneath, 3/four is larger than one/4. The larger the numerator, the larger the fraction.
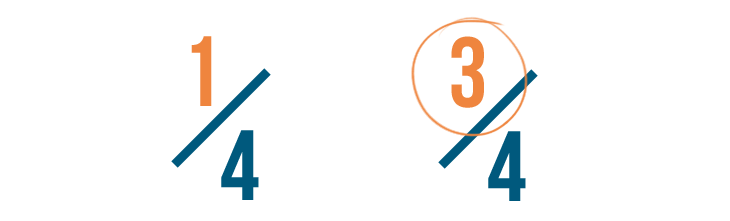
Comparison fractions with different denominators
On the previous page, we compared fractions that have the same lesser numbers, or denominators . Only yous know that fractions can have whatsoever number as a denominator. What happens when you lot need to compare fractions with different bottom numbers?
For case, which of these is larger: two/3 or i/5? Information technology's difficult to tell simply by looking at them. Later on all, 2 is larger than 1, simply the denominators aren't the same.
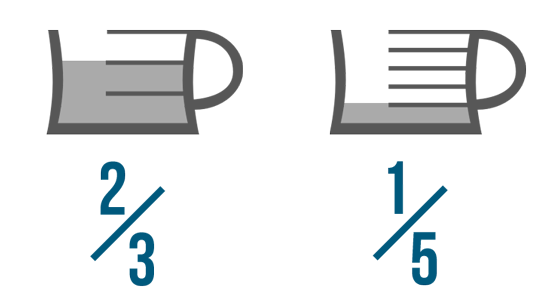
If yous await at the picture, though, the divergence is articulate: 2/3 is larger than 1/5. With an illustration, it was like shooting fish in a barrel to compare these fractions, only how could we have washed it without the picture?
Click through the slideshow to learn how to compare fractions with different denominators.
-
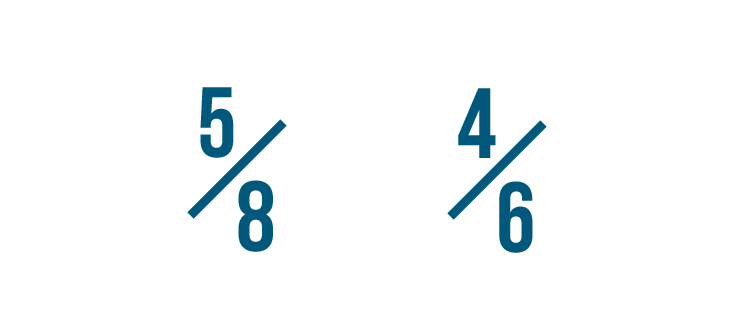
Permit'due south compare these fractions: 5/8 and 4/6.
-
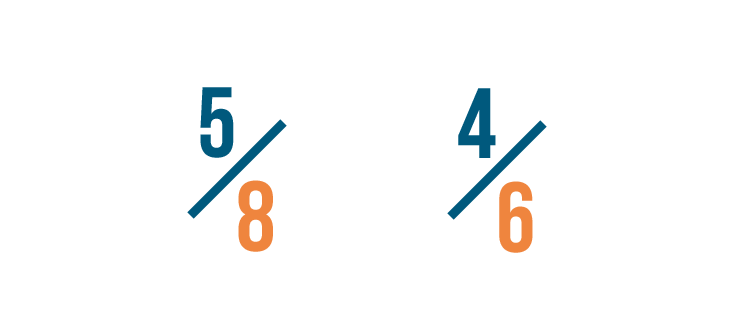
Earlier we compare them, we need to change both fractions so they have the same denominator, or bottom number.
-
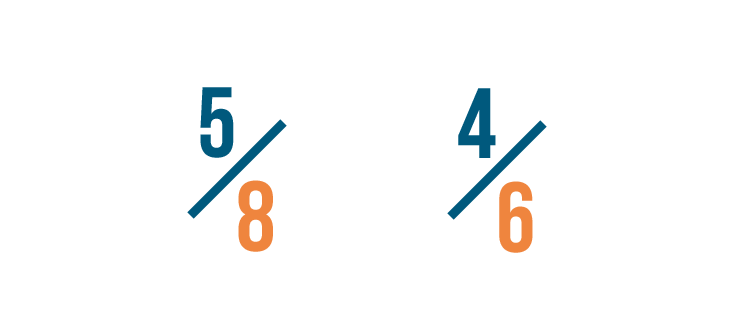
Starting time, we'll find the smallest number that can be divided past both denominators. We telephone call that the everyman common denominator.
-
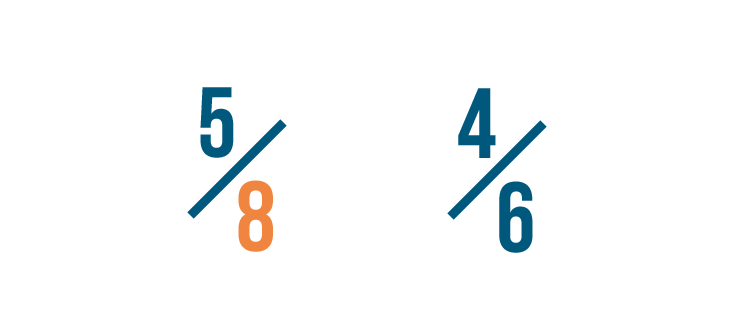
Our commencement pace is to find numbers that can be divided evenly past eight.
-

Using a multiplication table makes this easy. All of the numbers on the 8 row can be divided evenly by 8.
-
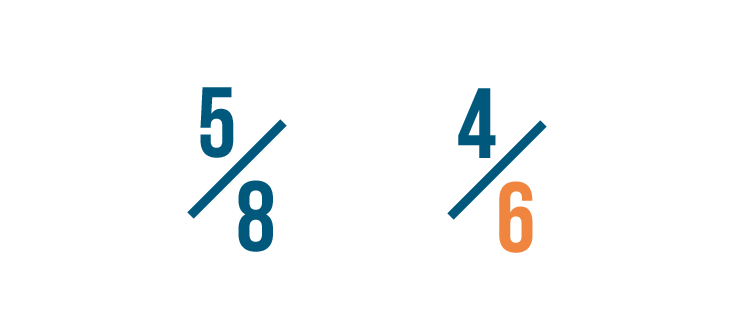
Now let's wait at our second denominator: six.
-

We can apply the multiplication tabular array again. All of the numbers in the 6 row tin can be divided evenly by 6.
-
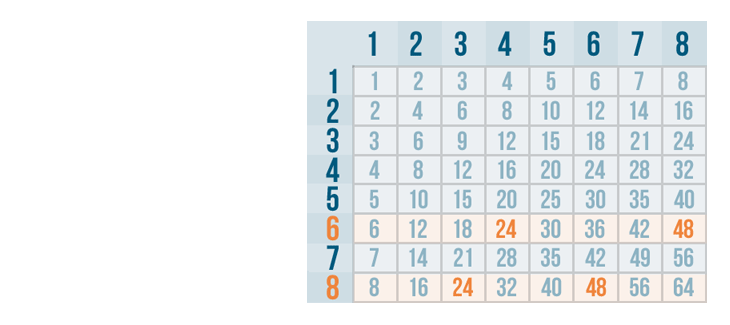
Let'southward compare the ii rows. Information technology looks like there are a few numbers that can be divided evenly past both half dozen and 8.
-
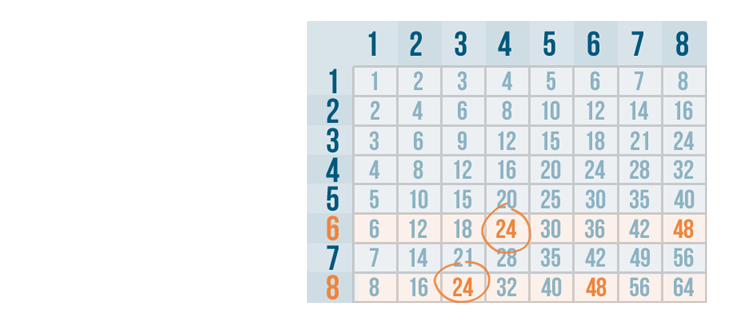
24 is the smallest number that appears on both rows, so it's the lowest common denominator.
-
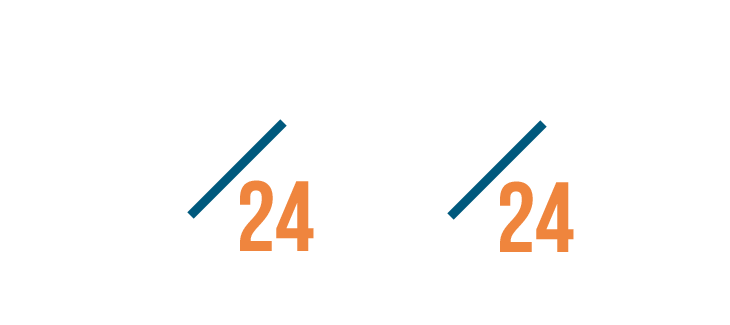
Now we're going to change our fractions then they both have the same denominator: 24.
-
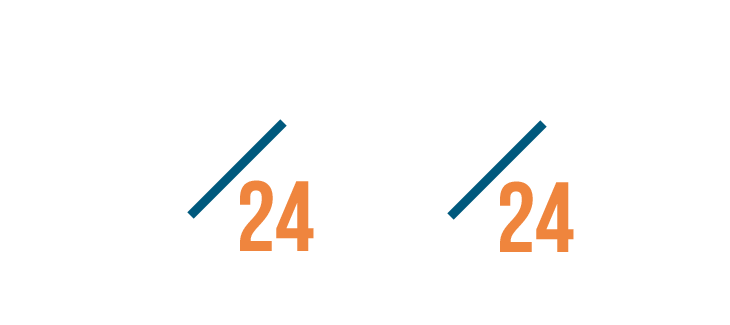
To do that, we'll have to alter the numerators the same mode nosotros inverse the denominators.
-
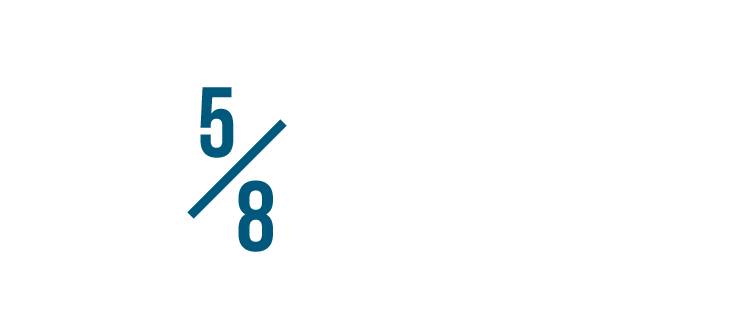
Allow's look at five/eight once more. In order to change the denominator to 24...
-
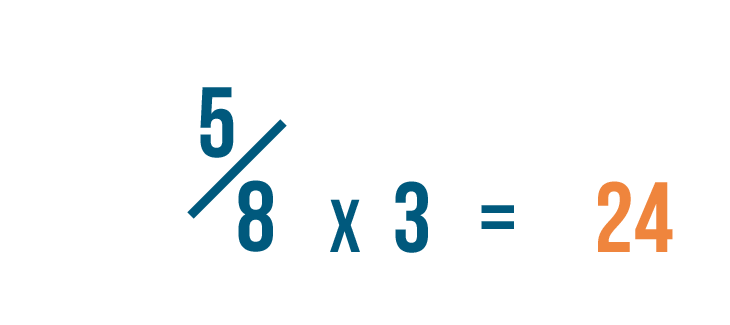
Let'southward wait at v/viii again. In order to change the denominator to 24...we had to multiply 8 past three.
-
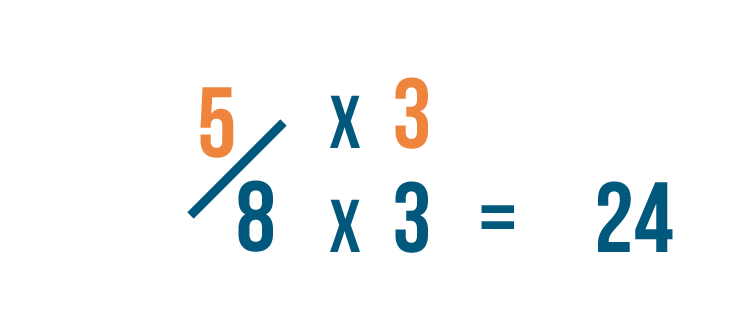
Since we multiplied the denominator by 3, we'll also multiply the numerator, or top number, past iii.
-
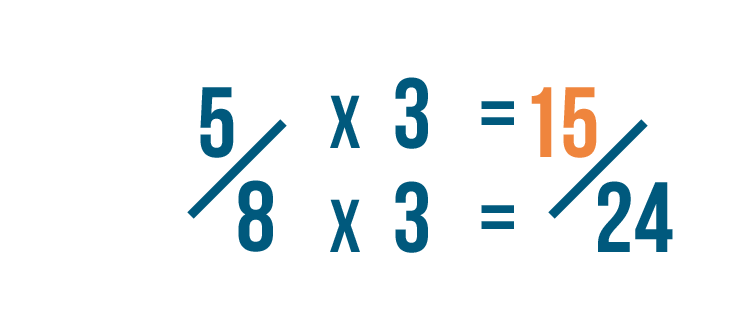
five times three equals 15. So we've changed 5/8 into fifteen/24.
-
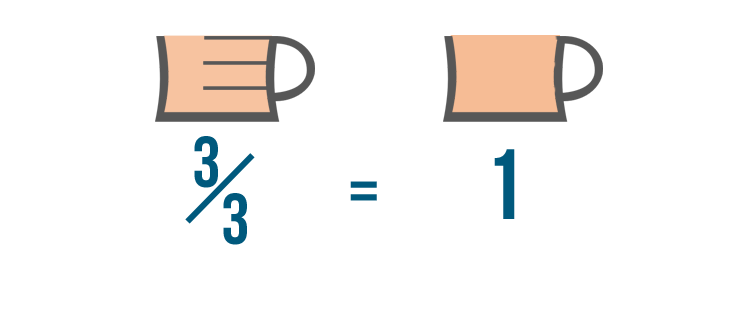
We tin do that because whatsoever number over itself is equal to 1.
-
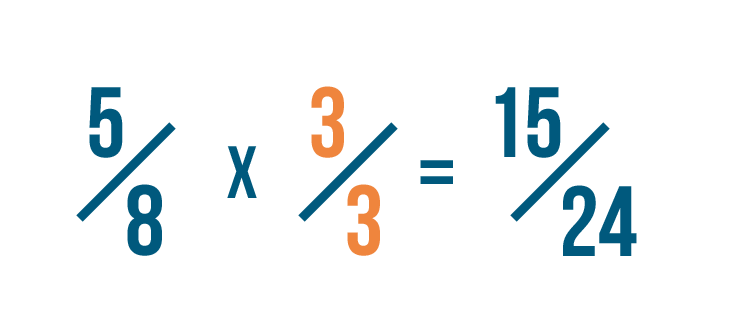
So when nosotros multiply v/8 past 3/iii...
-
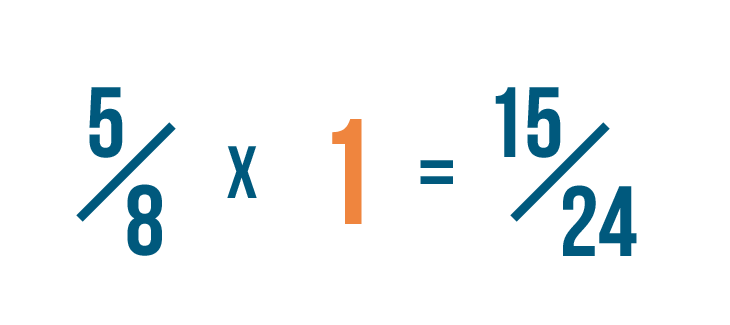
And then when we multiply 5/8 by iii/3...we're really multiplying 5/8 by 1.
-
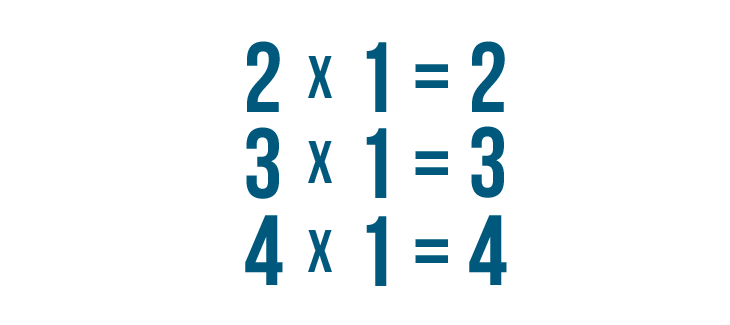
Since whatsoever number times 1 is equal to itself...
-
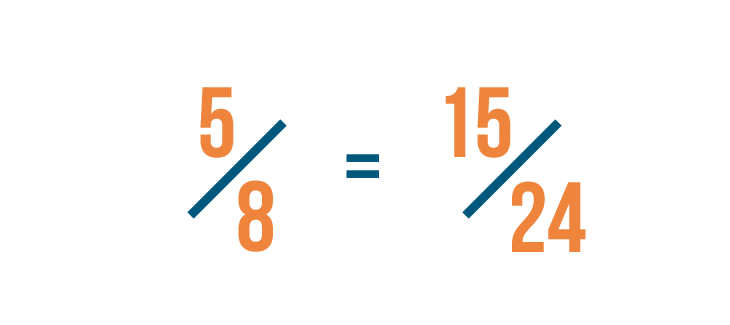
Since any number times one is equal to itself...we can say that 5/8 is equal to 15/24.
-
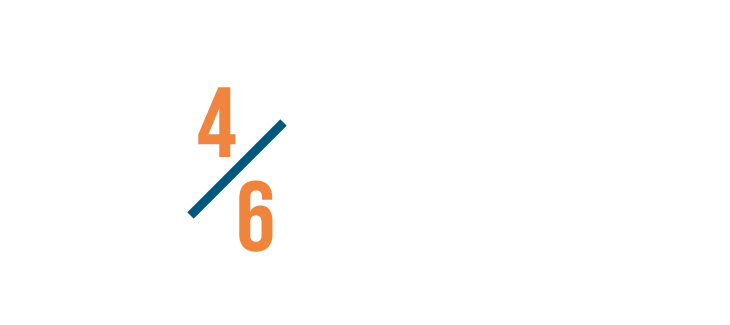
Now we'll do the aforementioned to our other fraction: 4/half-dozen. We likewise changed its denominator to 24.
-
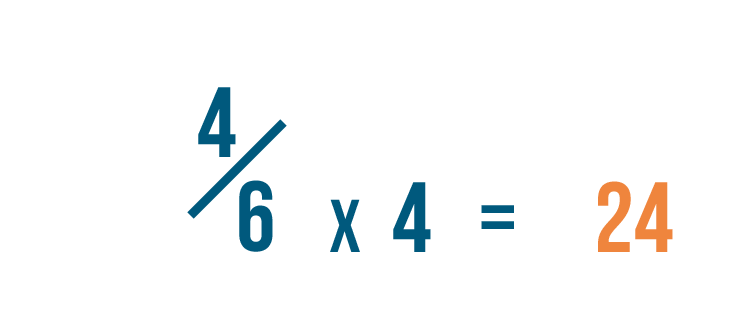
Our erstwhile denominator was half dozen. To go 24, we multiplied half-dozen by 4.
-
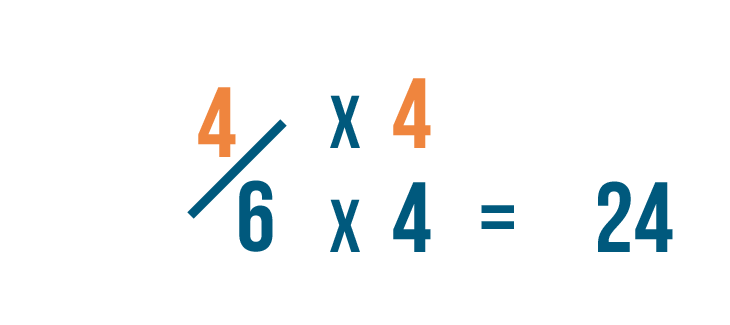
And then we'll likewise multiply the numerator by 4.
-
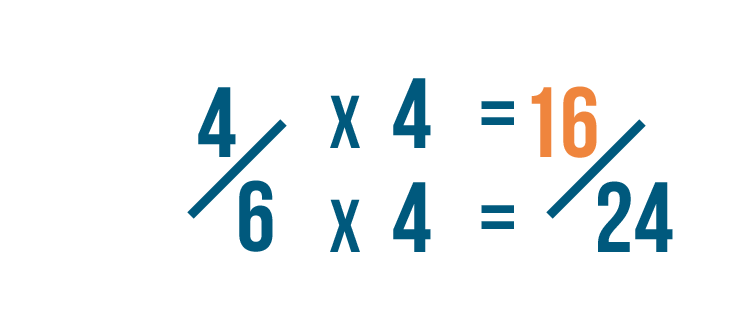
four times iv is 16. So 4/6 is equal to 16/24.
-
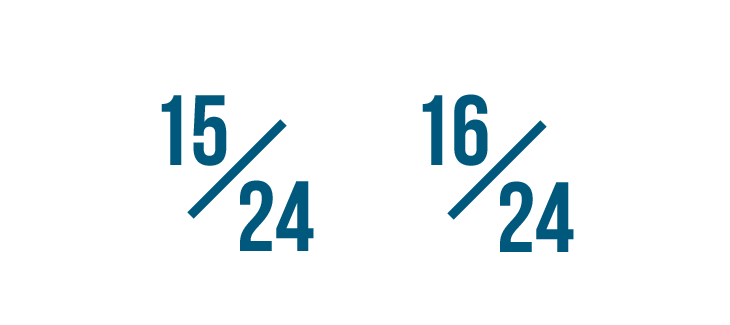
Now that the denominators are the aforementioned, we can compare the two fractions by looking at their numerators.
-
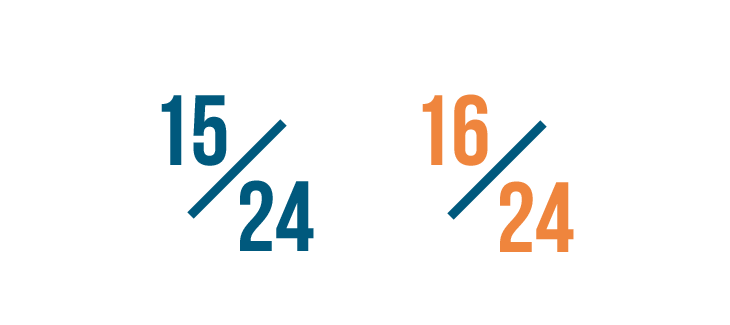
16/24 is larger than 15/24...
-
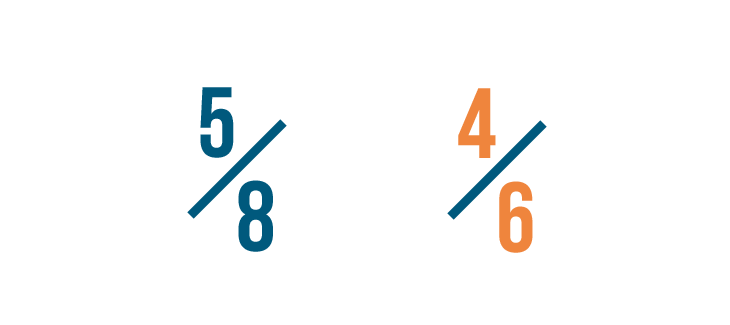
sixteen/24 is larger than 15/24... and so iv/half dozen is larger than v/viii.
-

Reducing fractions
Which of these is larger: 4/8 or one/2?

If you did the math or fifty-fifty simply looked at the picture, yous might take been able to tell that they're equal . In other words, 4/8 and i/2 mean the same thing, even though they're written differently.
If four/eight means the same thing as ane/2, why not just call it that? Half is easier to say than four-eighths, and for about people it's also easier to empathise. Later all, when you consume out with a friend, you separate the bill in one-half, not in eighths.
If you lot write iv/eight as one/2, you're reducing information technology. When nosotros reduce a fraction, we're writing it in a simpler grade. Reduced fractions are always equal to the original fraction.
We already reduced 4/eight to 1/two. If you look at the examples below, you can run across that other numbers can exist reduced to one/two also. These fractions are all equal.
v/10 = 1/211/22 = 1/2
36/72 = 1/two
These fractions accept all been reduced to a simpler class as well.
4/12 = one/314/21 = 2/3
35/50 = seven/x
Click through the slideshow to learn how to reduce fractions by dividing.
-

Let's endeavour reducing this fraction: 16/xx.
-
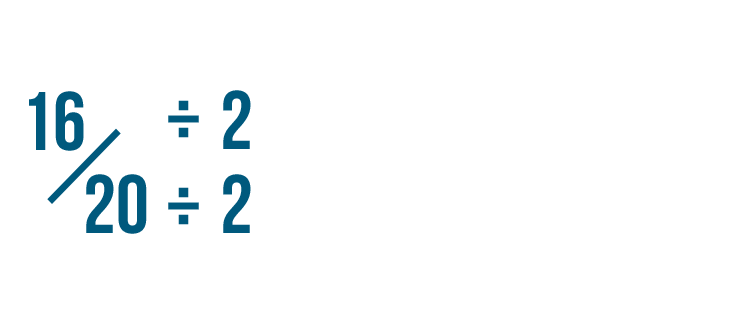
Since the numerator and denominator are even numbers, you can divide them by 2 to reduce the fraction.
-
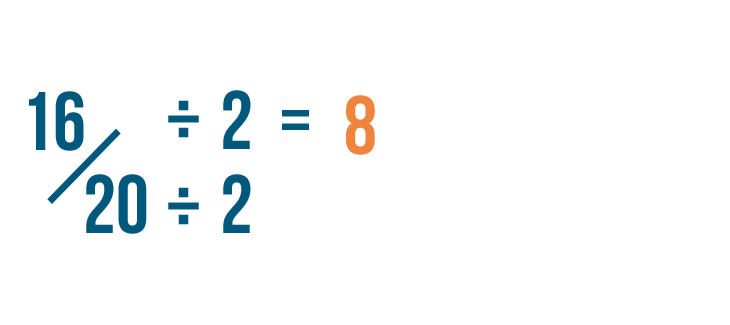
First, nosotros'll separate the numerator by ii. 16 divided by 2 is 8.
-
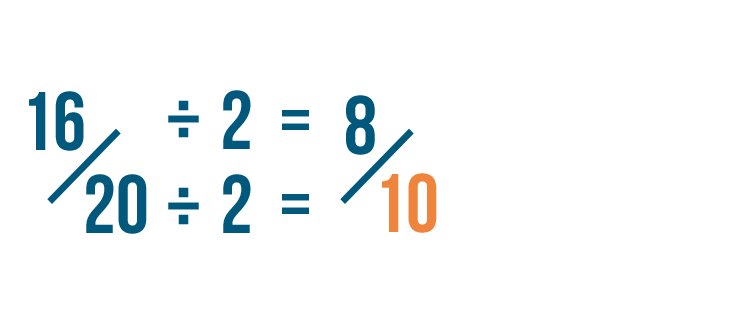
Next, we'll dissever the denominator by ii. twenty divided by ii is x.
-
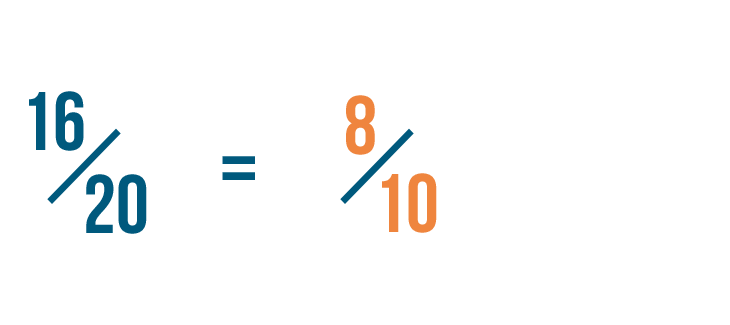
Nosotros've reduced 16/twenty to eight/ten. We could also say that 16/20 is equal to eight/10.
-
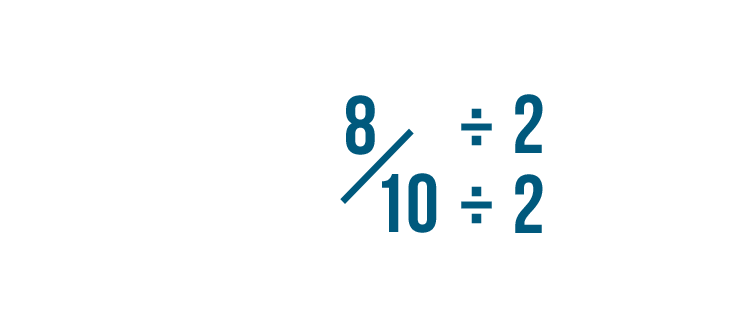
If the numerator and denominator tin withal be divided past ii, we can go on reducing the fraction.
-
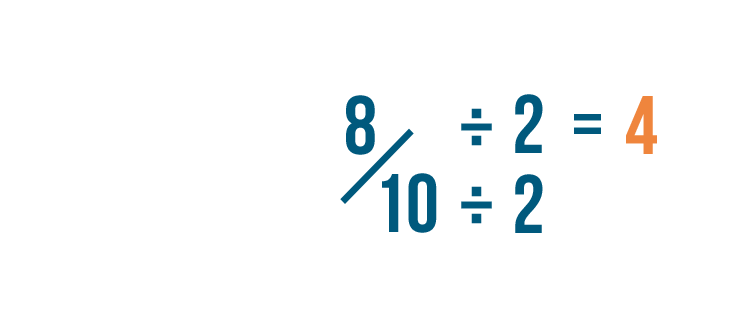
8 divided past 2 is 4.
-
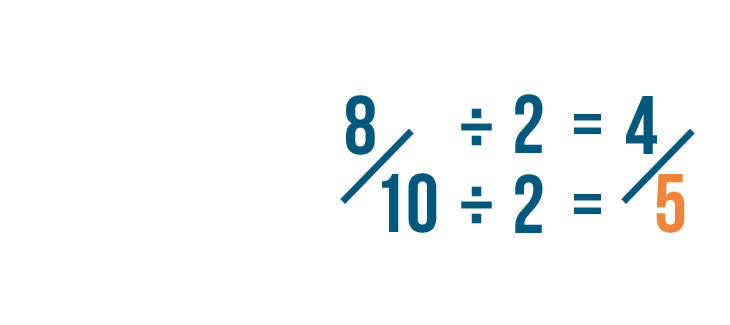
10 divided past 2 is five.
-

Since there's no number that 4 and 5 tin be divided by, we tin't reduce 4/5 whatsoever farther.
-
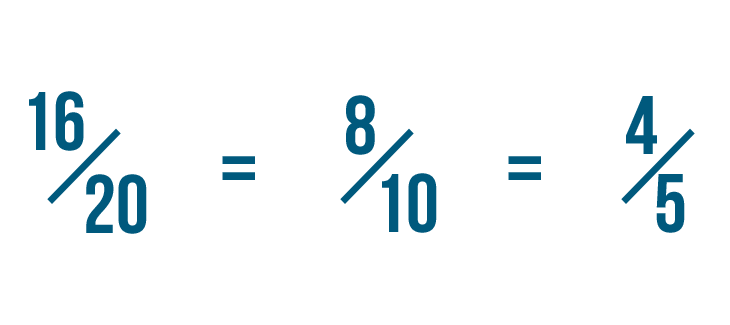
This means 4/5 is the simplest form of 16/xx.
-

Let's try reducing another fraction: half-dozen/nine.
-

While the numerator is even, the denominator is an odd number, so we can't reduce by dividing by two.
-
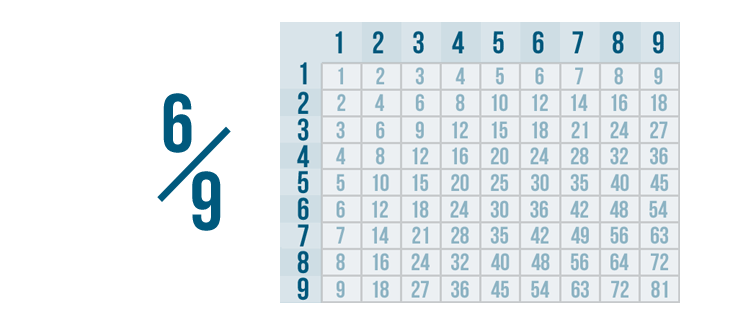
Instead, we'll need to find a number that 6 and 9 can exist divided past. A multiplication table will brand that number piece of cake to find.
-
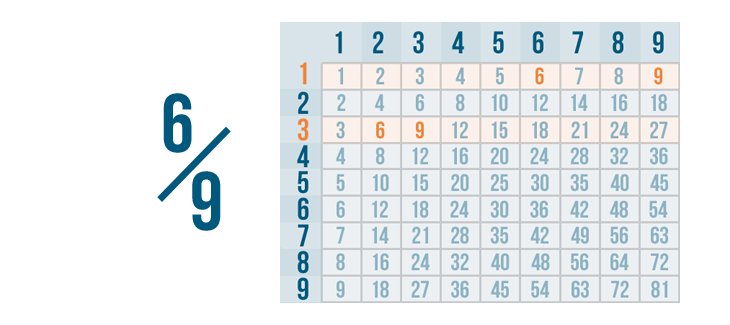
Permit's find six and 9 on the aforementioned row. As yous can come across, 6 and ix can both be divided by 1 and three.
-

Dividing by 1 won't change these fractions, and then we'll use the largest number that 6 and 9 tin can be divided past.
-
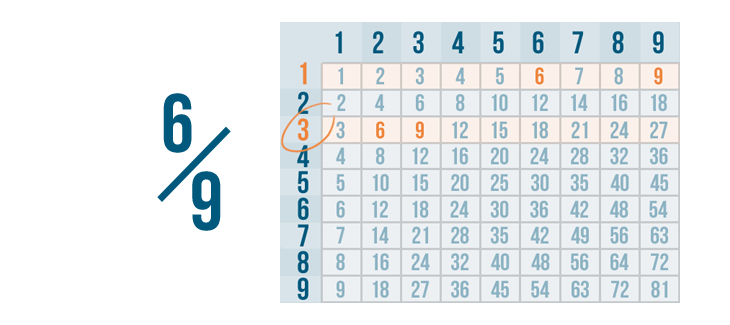
That's 3. This is called the greatest mutual divisor, or GCD. (Y'all can also call it the greatest common gene, or GCF.)
-

3 is the GCD of 6 and 9 because it'south the largest number they can be divided by.
-
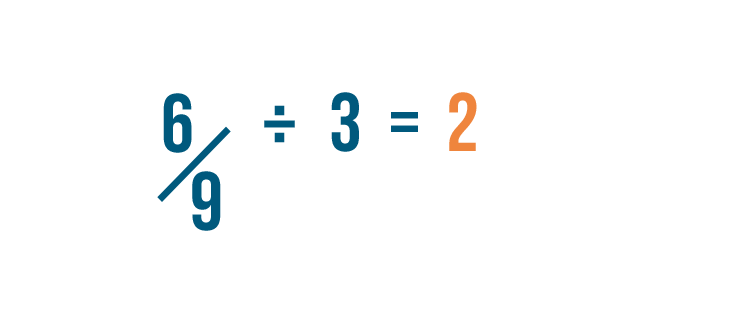
Then we'll divide the numerator by 3. 6 divided past iii is 2.
-
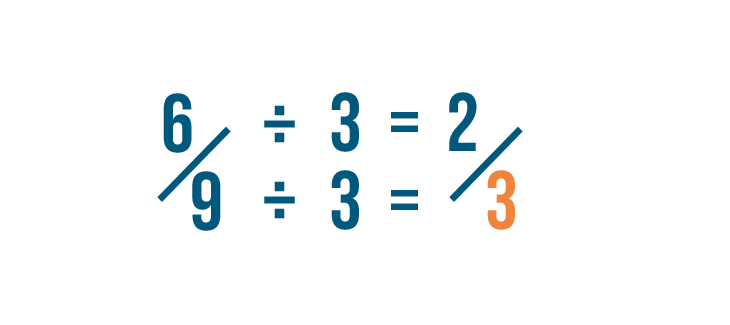
Then we'll separate the denominator by 3. 9 divided by 3 is 3.
-
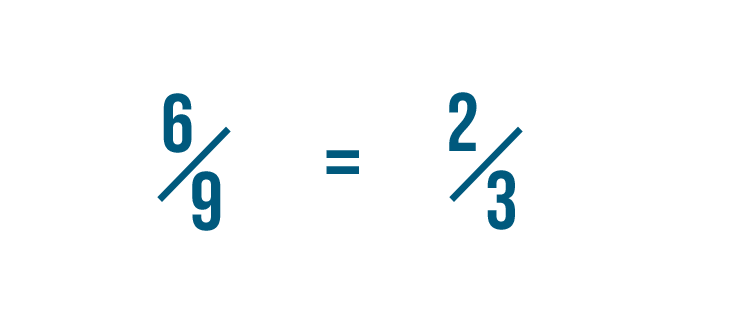
Now we've reduced six/9 to two/3, which is its simplest form. We could as well say that six/9 is equal to two/3.
-

Irreducible fractions
Non all fractions tin be reduced. Some are already equally simple as they can be. For instance, you tin't reduce 1/two because there's no number other than ane that both 1 and ii can be divided by. (For that reason, you tin't reduce whatever fraction that has a numerator of 1.)
Some fractions that accept larger numbers can't be reduced either. For instance, 17/36 tin can't be reduced considering there's no number that both 17 and 36 tin can be divided by. If you tin't find any common multiples for the numbers in a fraction, chances are information technology'due south irreducible .
Try This!
Reduce each fraction to its simplest grade.
Mixed numbers and improper fractions
In the previous lesson, you learned about mixed numbers. A mixed number has both a fraction and a whole number. An example is i 2/three. You'd read 1 ii/3 like this: one and 2-thirds.
Another fashion to write this would exist 5/3, or five-thirds. These ii numbers await different, but they're really the same. 5/three is an improper fraction. This just means the numerator is larger than the denominator.
There are times when yous may prefer to use an improper fraction instead of a mixed number. It's like shooting fish in a barrel to change a mixed number into an improper fraction. Allow'due south acquire how:
-
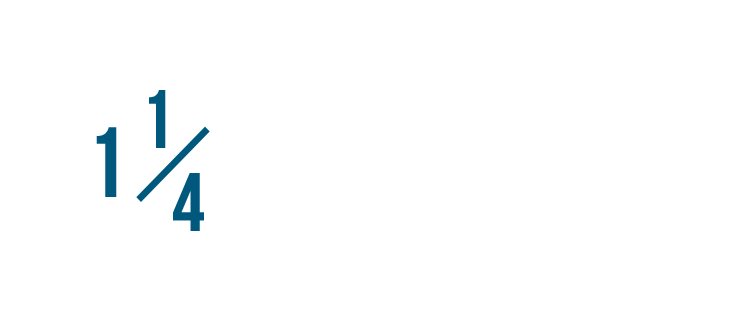
Let'southward convert 1 one/4 into an improper fraction.
-

Showtime, we'll demand to find out how many parts brand up the whole number: 1 in this example.
-
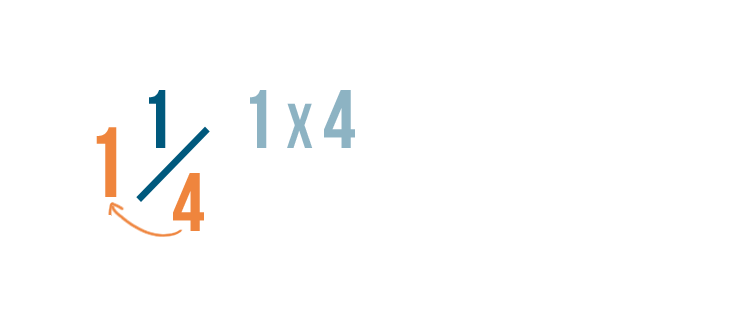
To do this, nosotros'll multiply the whole number, 1, by the denominator, 4.
-
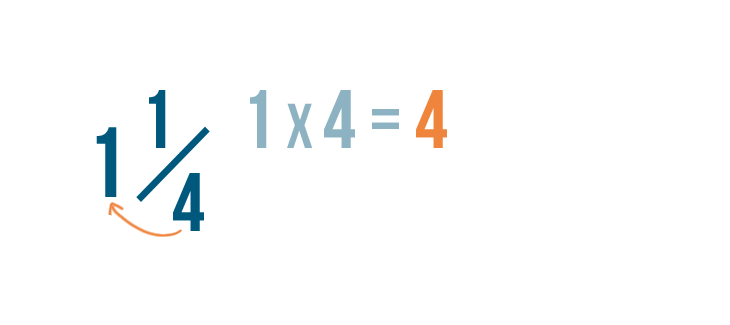
1 times 4 equals four.
-
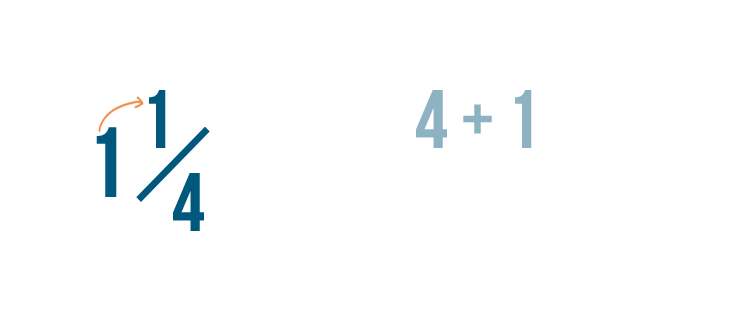
At present, let's add that number, 4, to the numerator, 1.
-
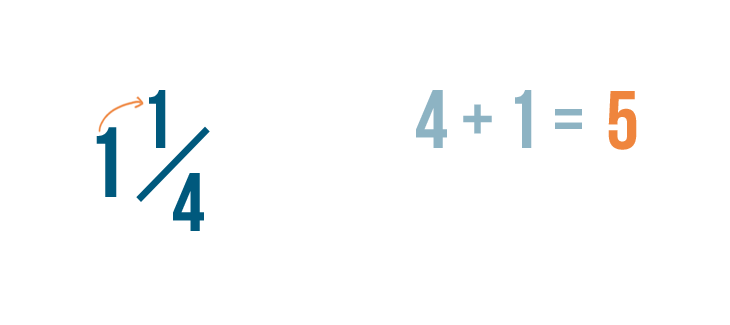
4 plus one equals 5.
-

The denominator stays the same.
-
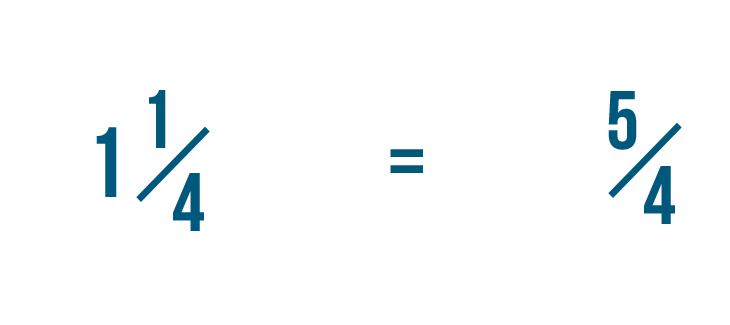
Our improper fraction is 5/4, or five-fourths. So we could say that one 1/4 is equal to five/iv.
-
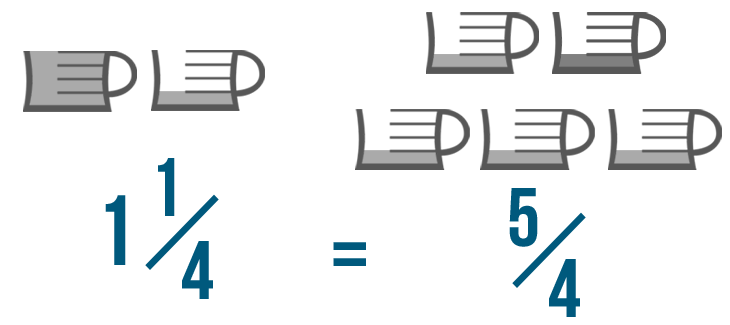
This means there are five 1/ivs in 1 1/4.
-

Permit's convert some other mixed number: two ii/5.
-
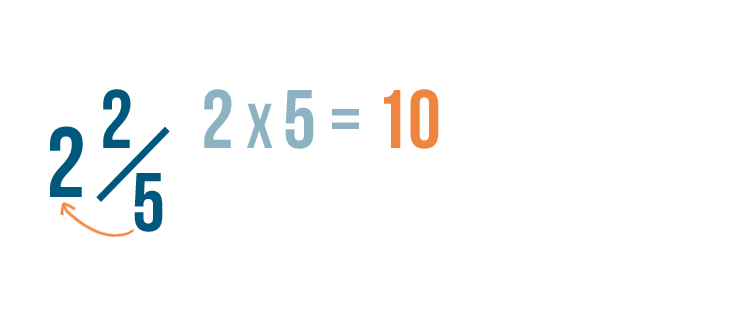
First, we'll multiply the whole number by the denominator. 2 times 5 equals 10.
-
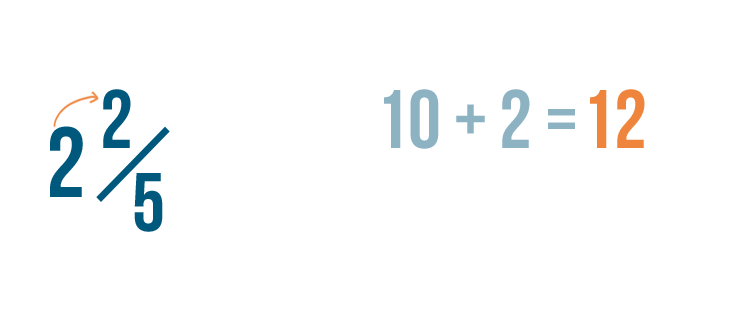
Next, nosotros'll add ten to the numerator. ten plus ii equals 12.
-

As always, the denominator will stay the same.
-
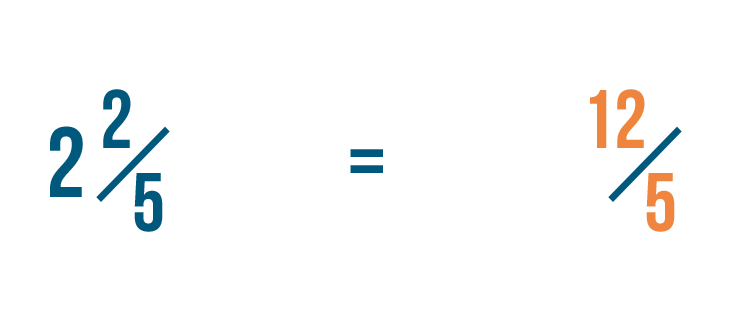
And so 2 2/5 is equal to 12/5.
-

Try This!
Try converting these mixed numbers into improper fractions.
Converting improper fractions into mixed numbers
Improper fractions are useful for math problems that use fractions, as yous'll learn later. However, they're besides more difficult to read and sympathise than mixed numbers. For example, it's a lot easier to picture show ii 4/7 in your head than eighteen/vii.
Click through the slideshow to learn how to change an improper fraction into a mixed number.
-

Let's turn 10/4 into a mixed number.
-
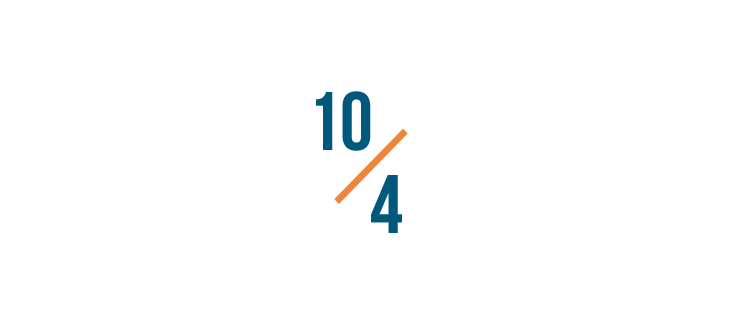
You tin can think of any fraction as a sectionalization problem. Just care for the line between the numbers like a segmentation sign (/).
-

So we'll carve up the numerator, 10, by the denominator, 4.
-
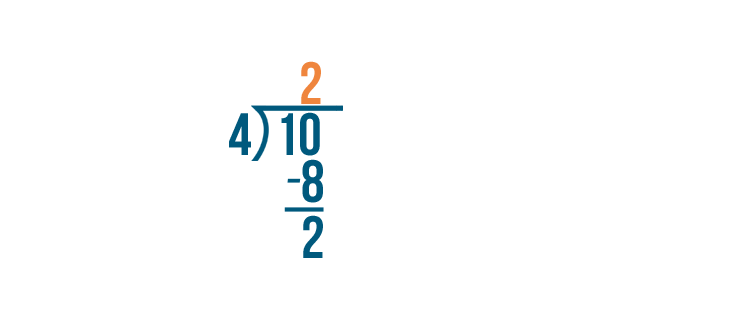
10 divided by iv equals 2...
-
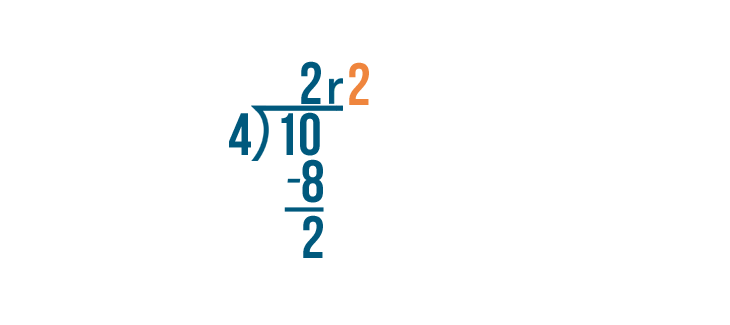
ten divided past iv equals ii... with a balance of 2.
-
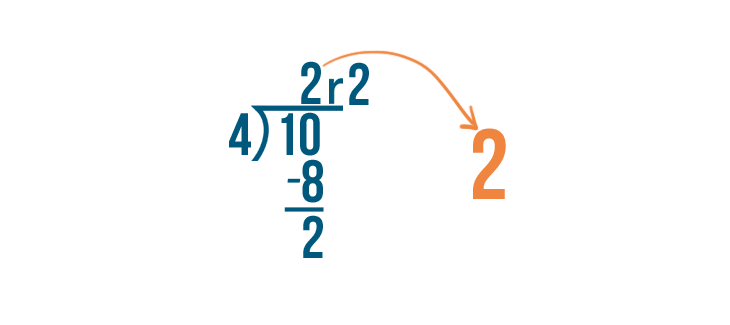
The answer, 2, volition become our whole number because x can exist divided by four twice.
-
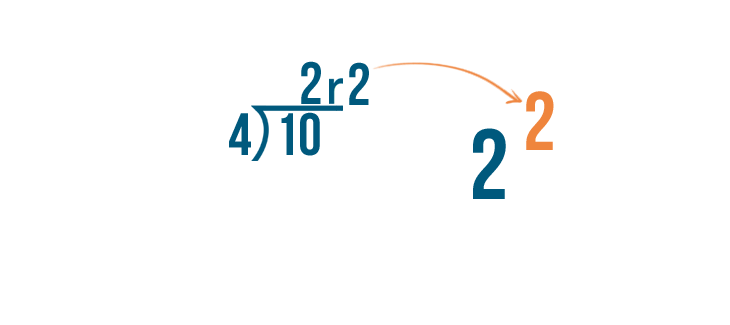
And the remainder, 2, will become the numerator of the fraction because we have 2 parts left over.
-
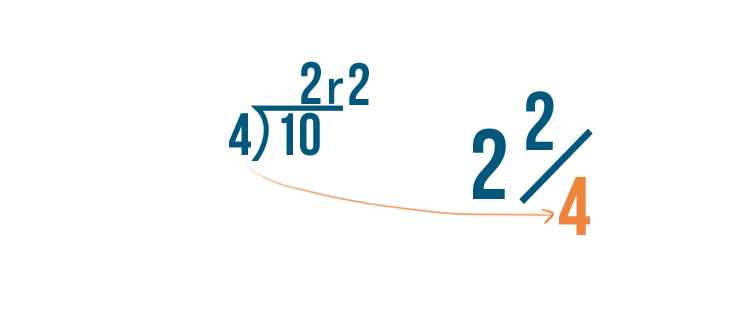
The denominator remains the same.
-
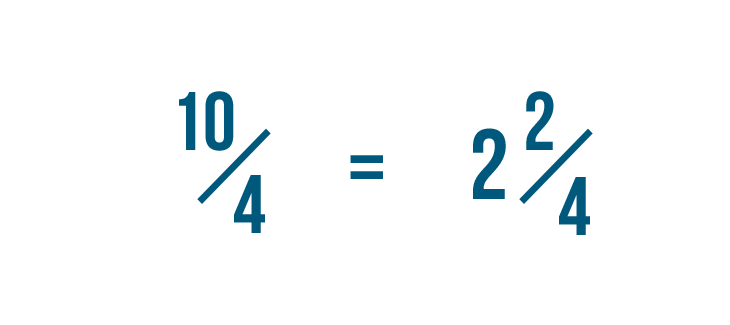
Then x/four equals 2 2/4.
-
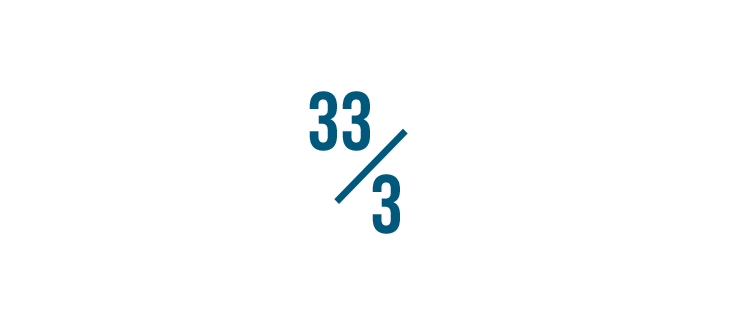
Let's endeavor some other example: 33/three.
-
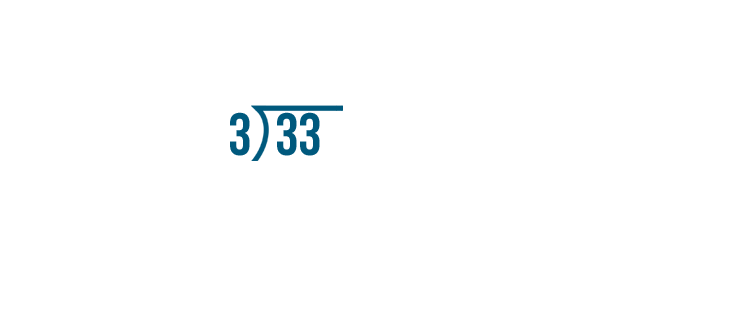
We'll divide the numerator, 33, past the denominator, 3.
-
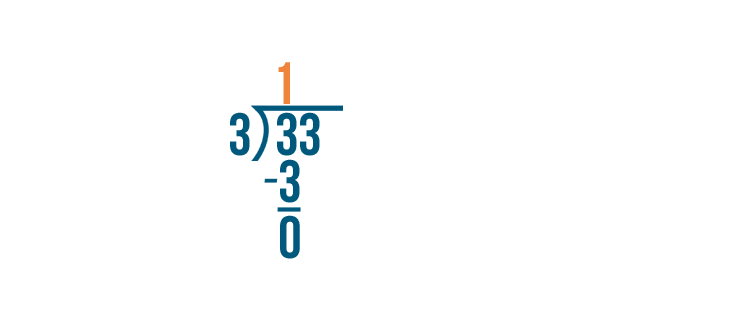
33 divided by 3...
-
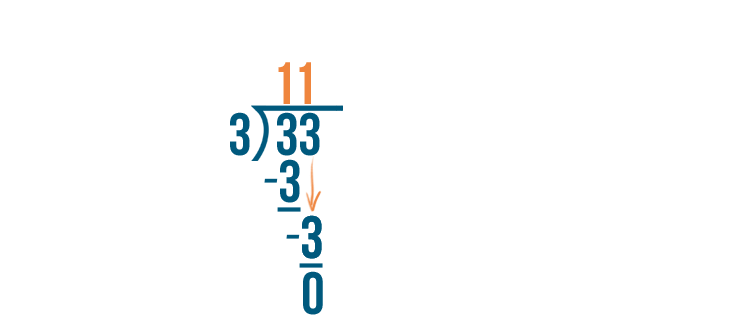
33 divided by 3... equals 11, with no balance.
-
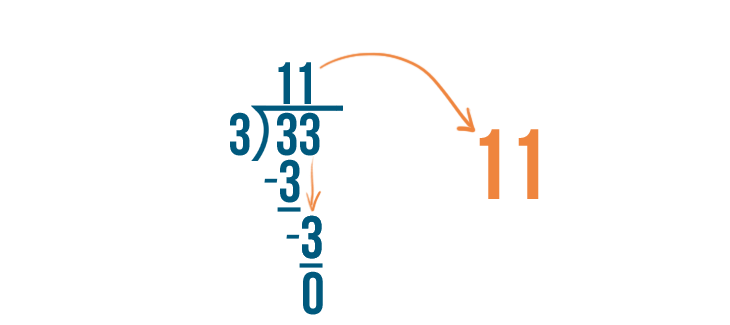
The respond, 11, volition become our whole number.
-
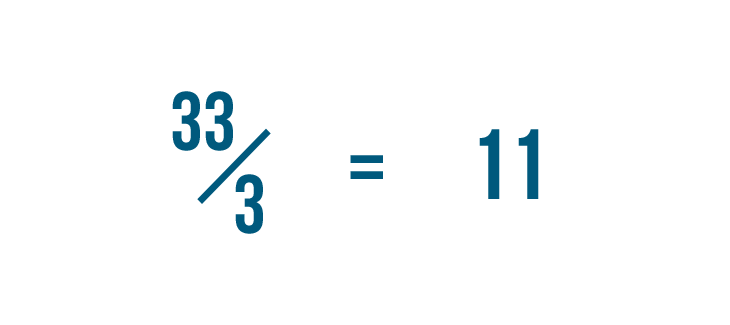
At that place is no residuum, so we tin come across that our improper fraction was actually a whole number. 33/three equals xi.
-

Endeavor This!
Try converting these improper fractions into mixed numbers.
/en/fractions/adding-and-subtracting-fractions/content/



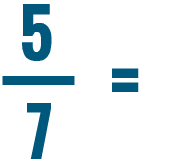
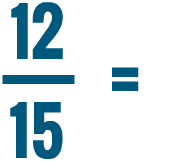
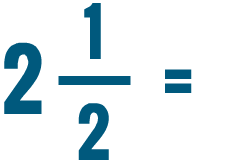
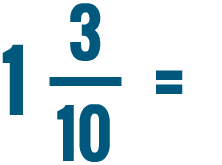




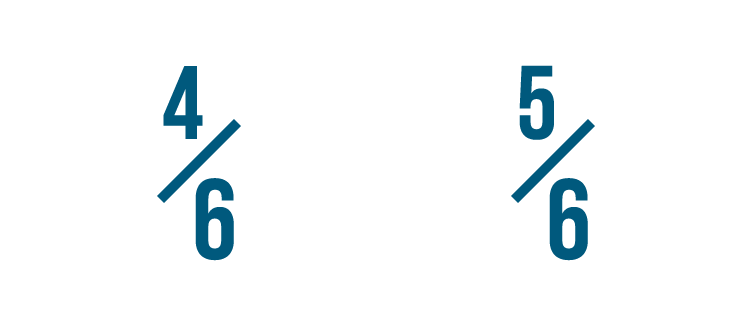








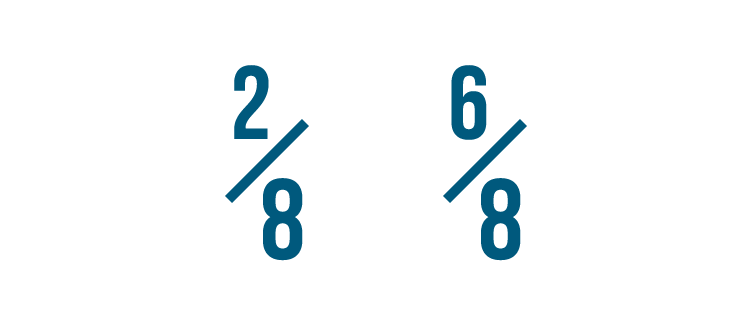
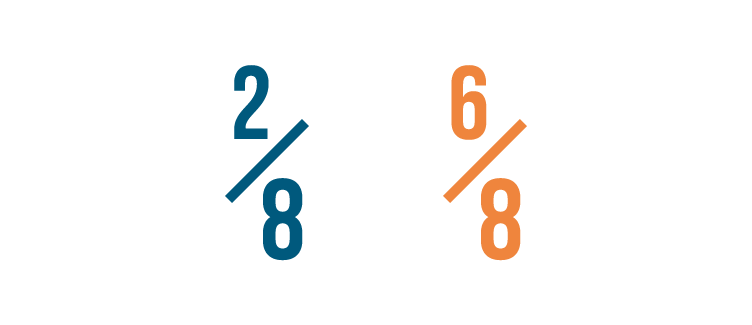
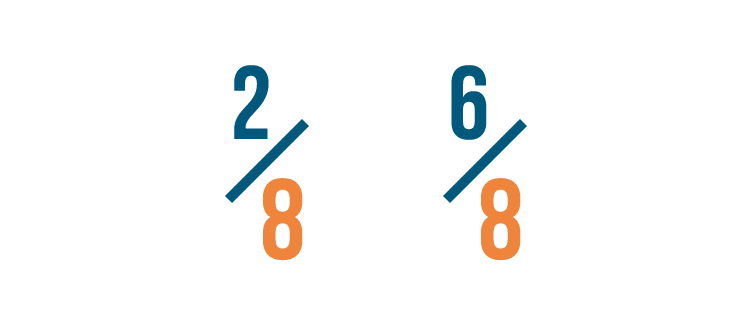
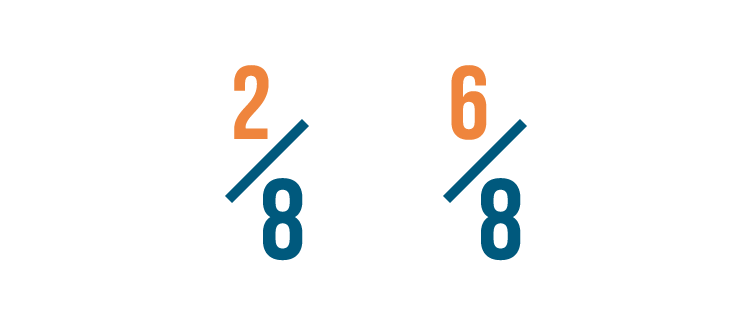

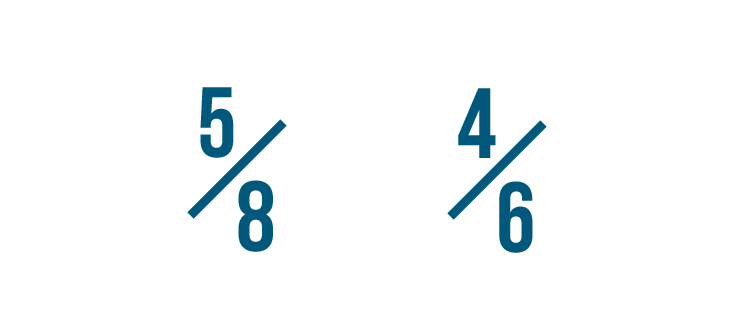

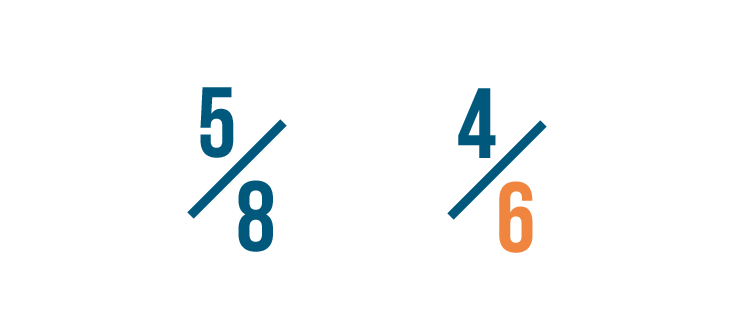



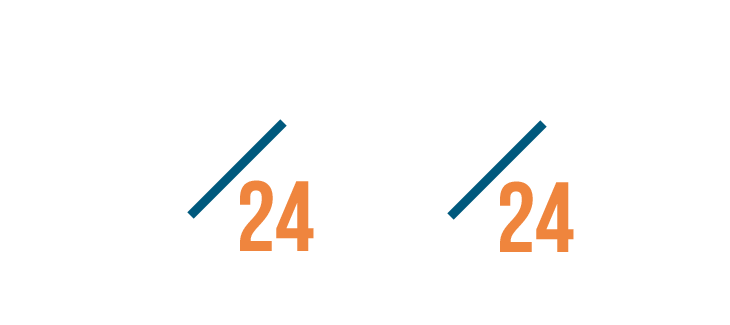
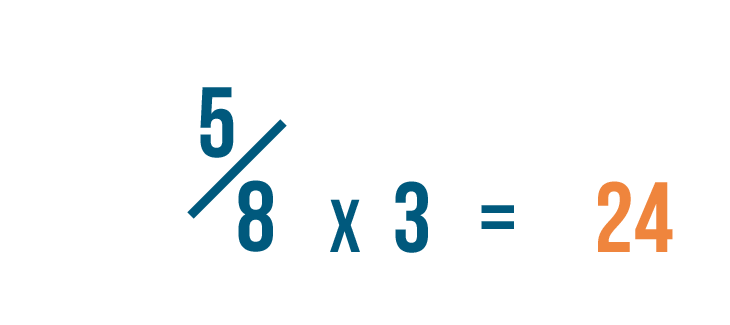
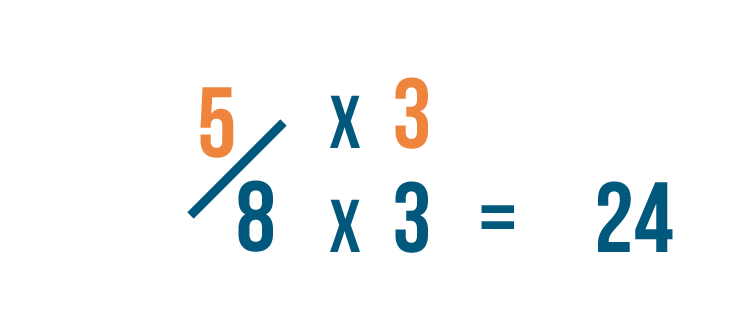
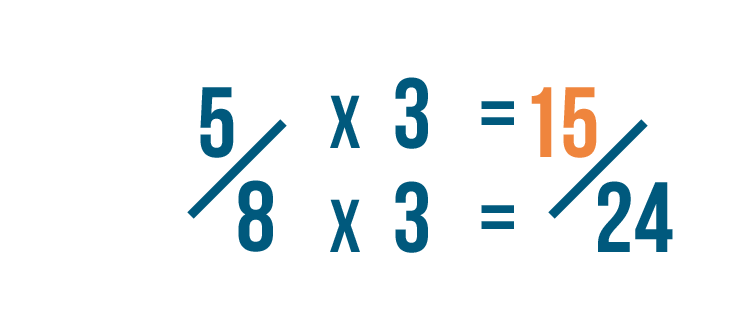
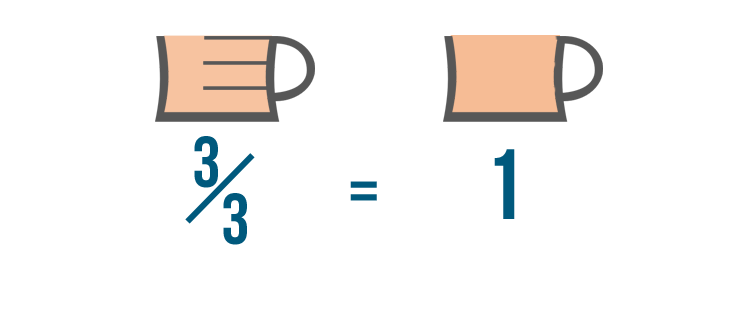
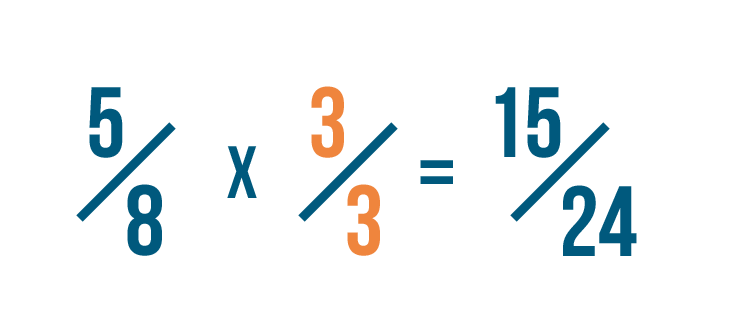
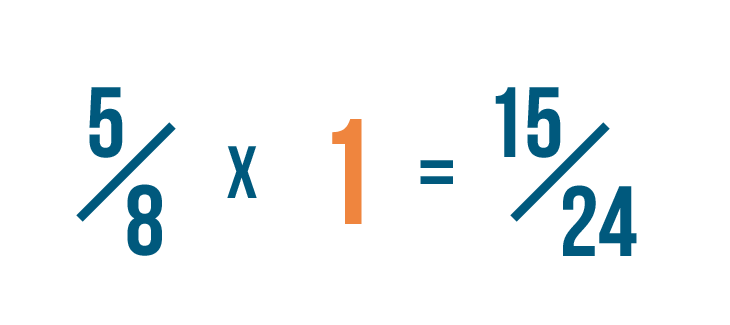
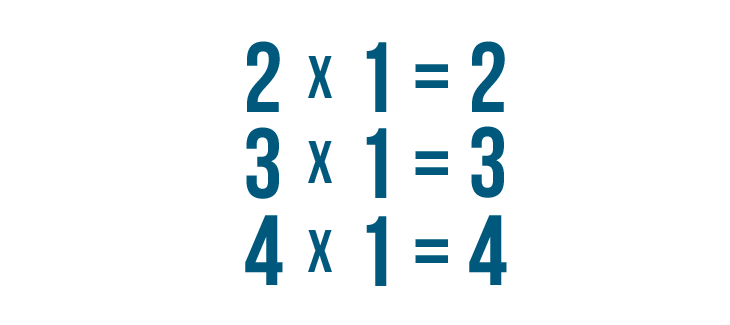
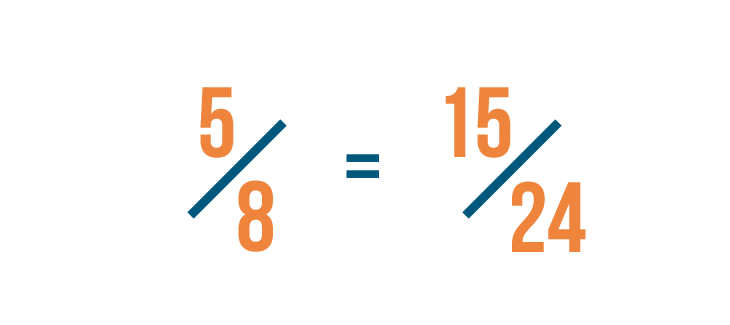
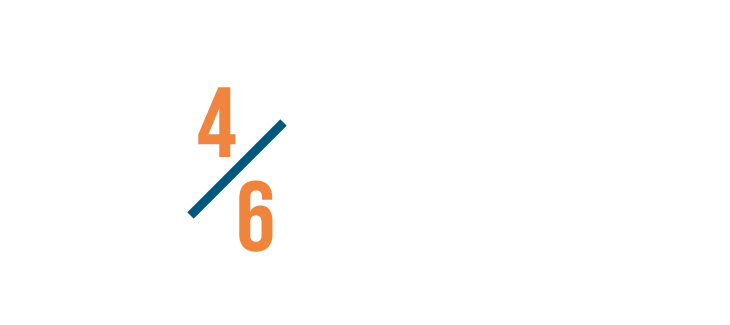
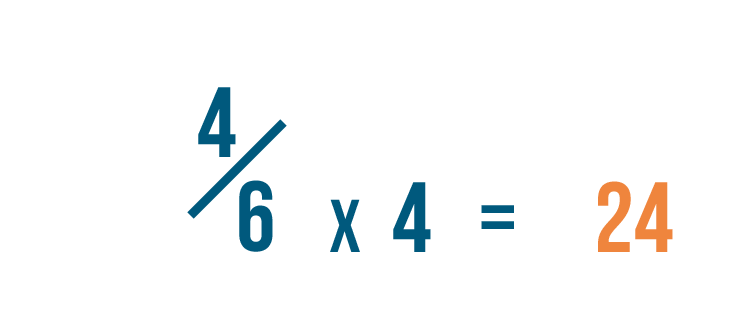
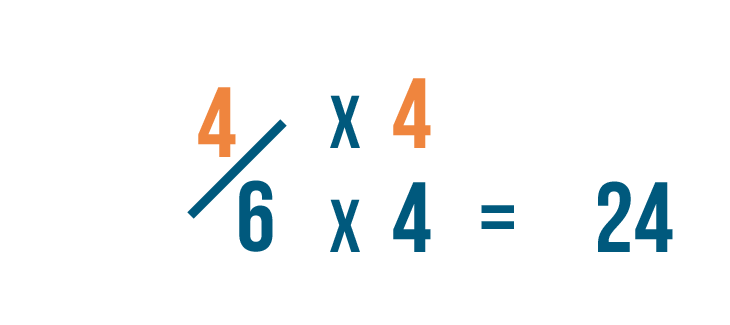
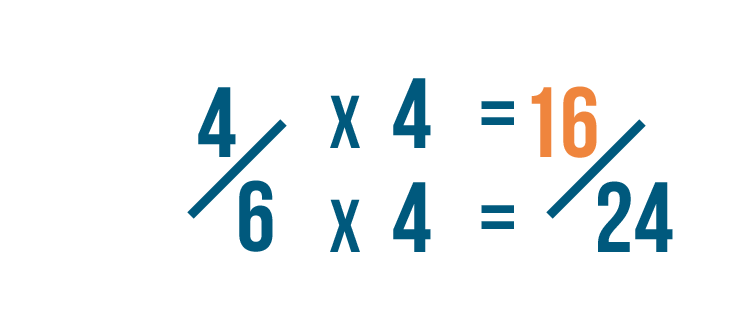
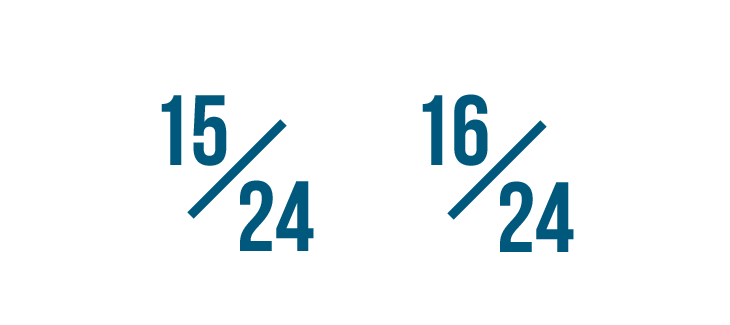
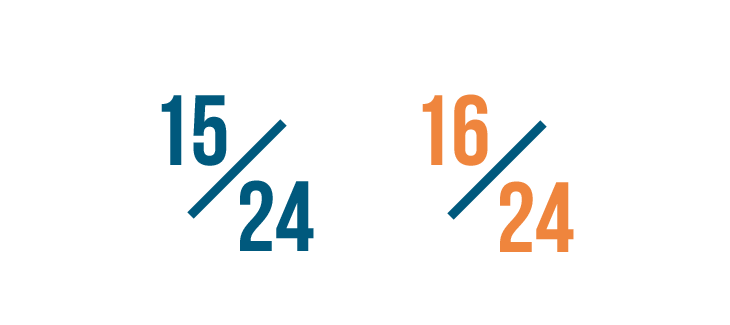
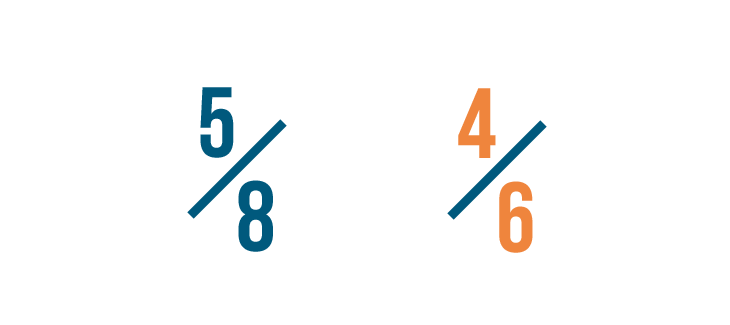

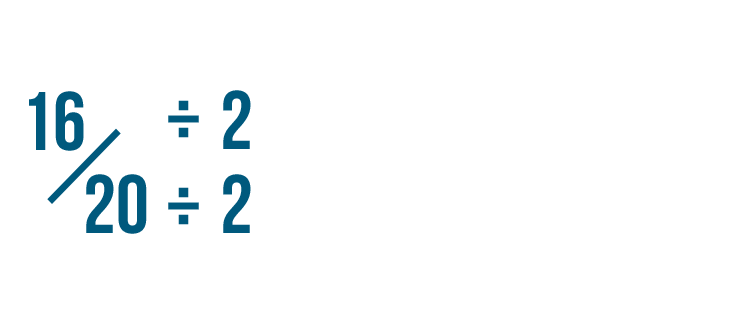
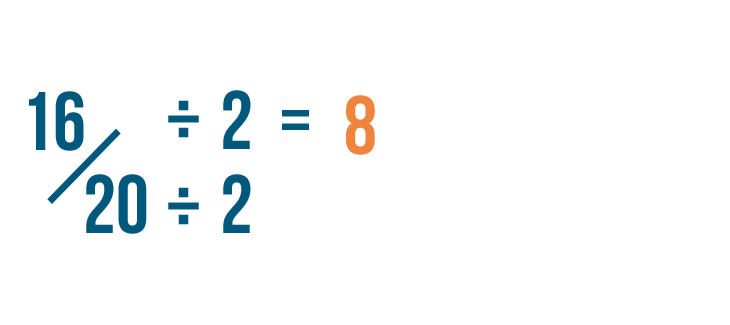
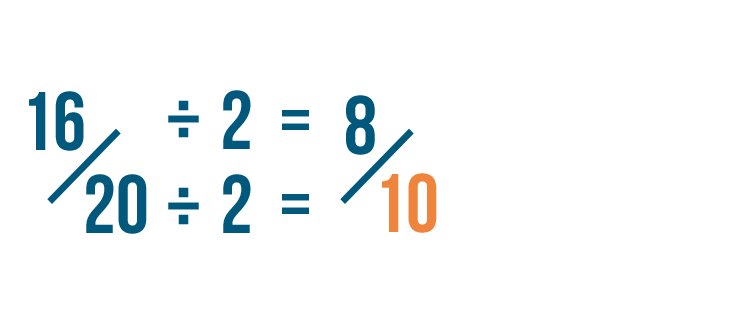
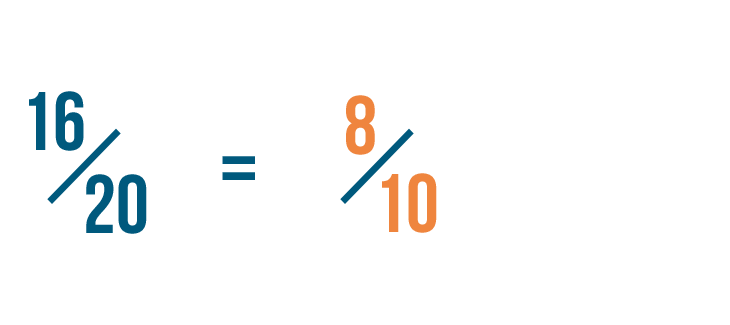
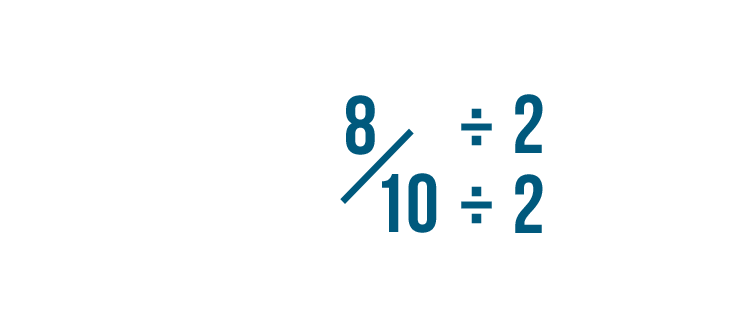
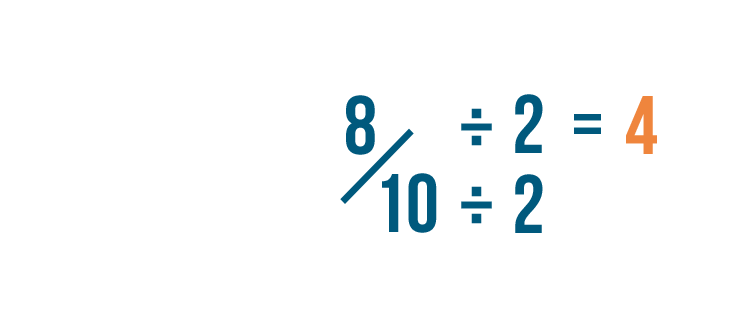
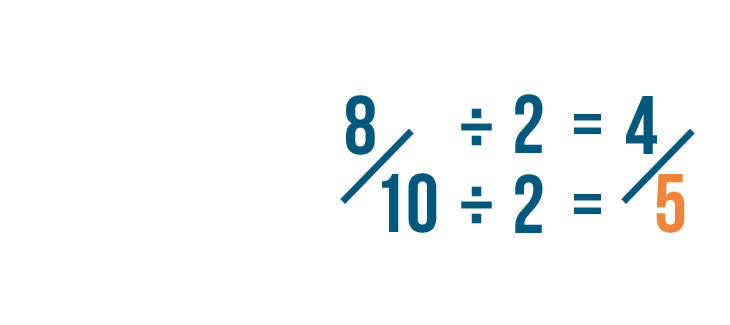

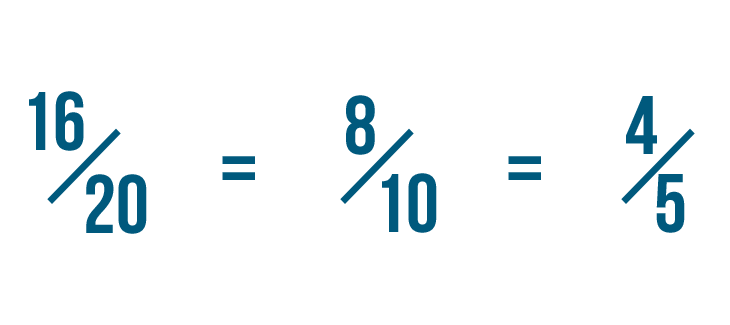





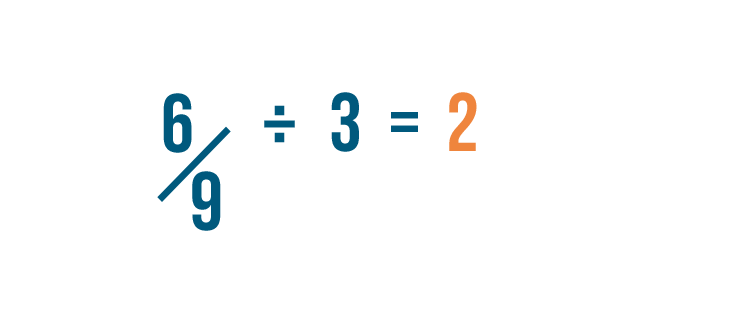
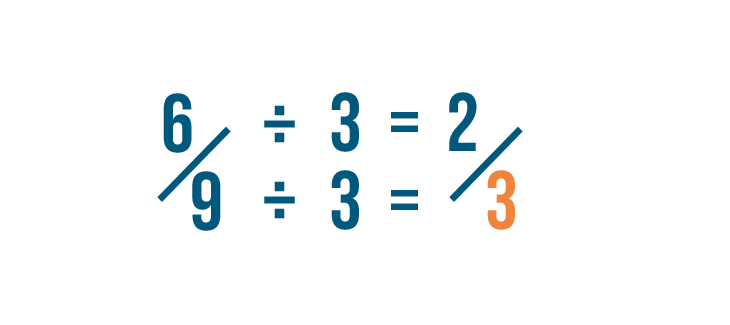
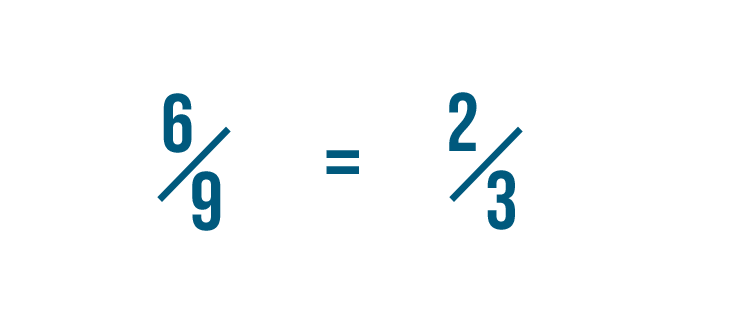
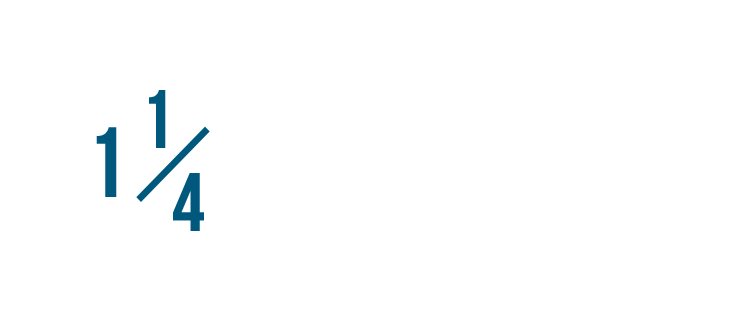

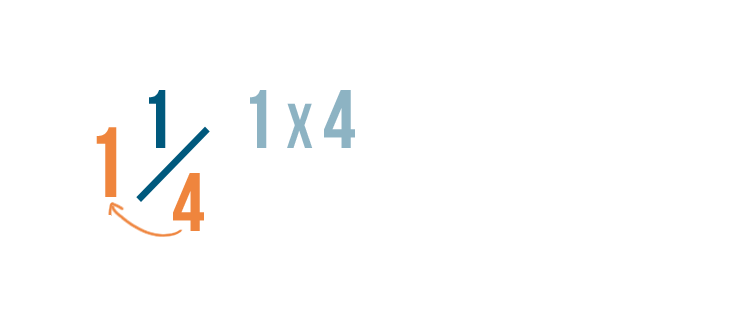
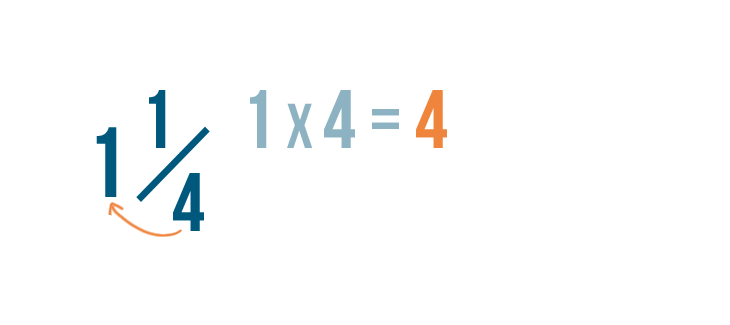
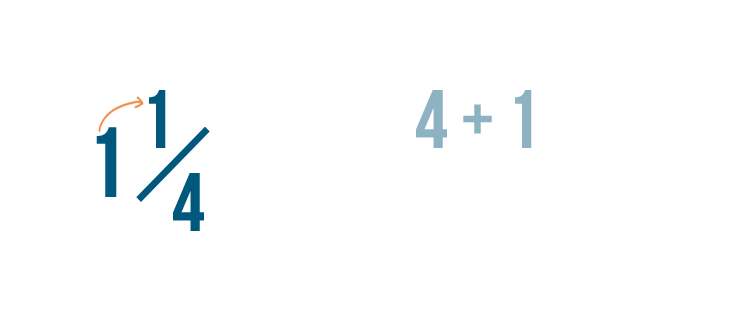
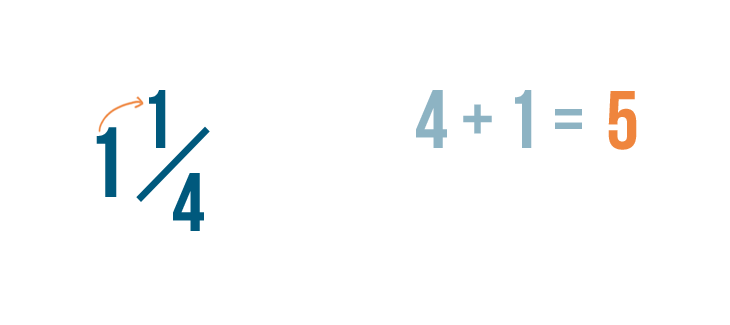

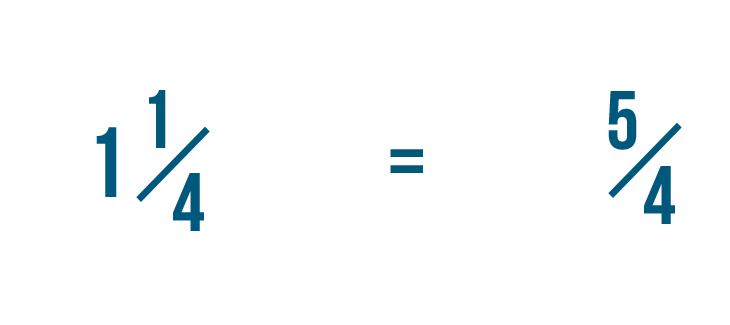
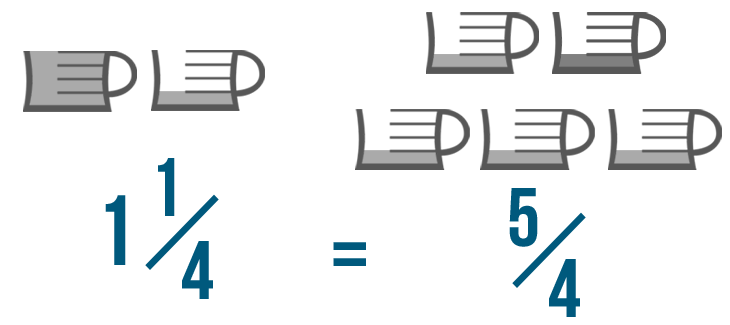

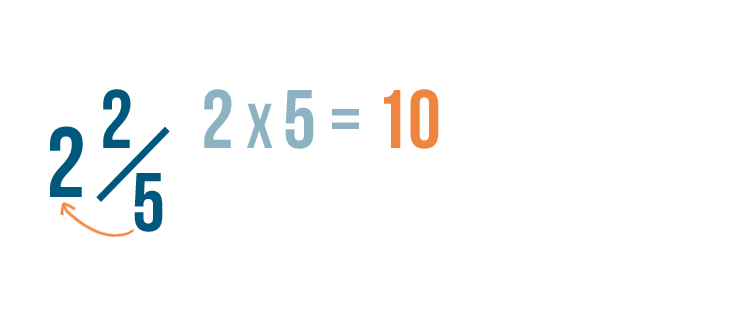
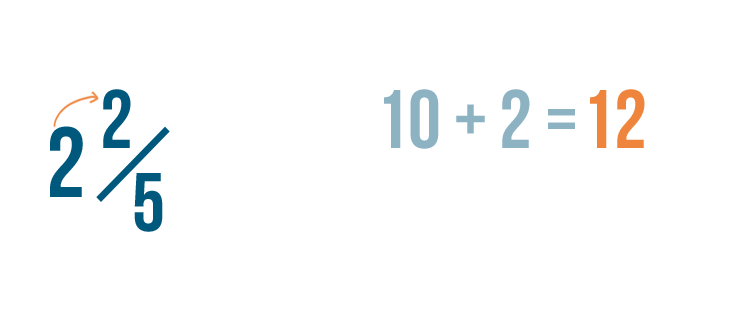

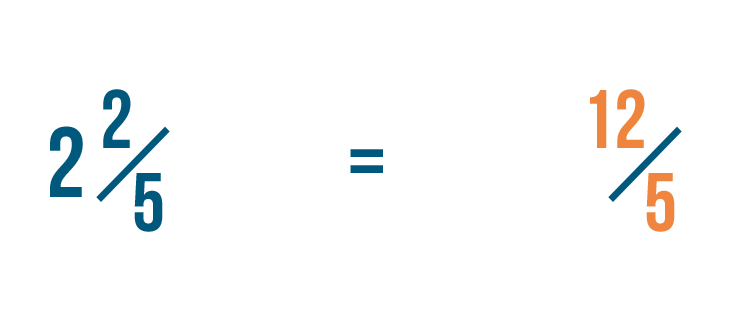

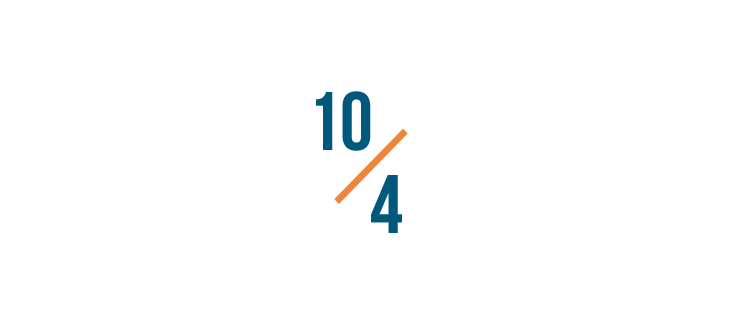

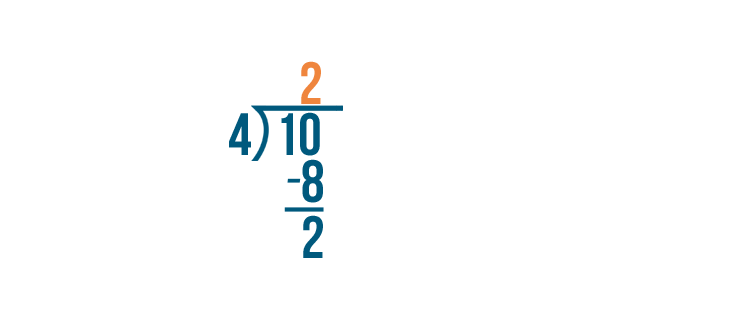
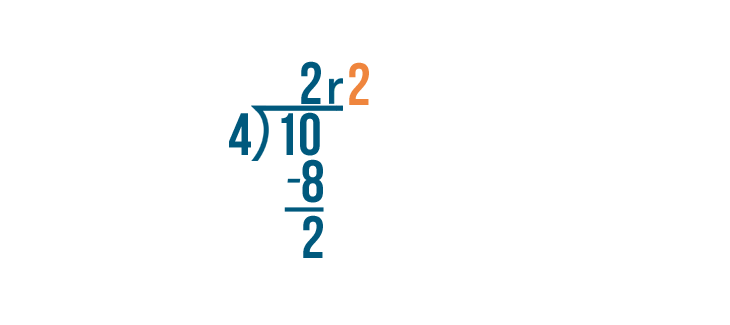
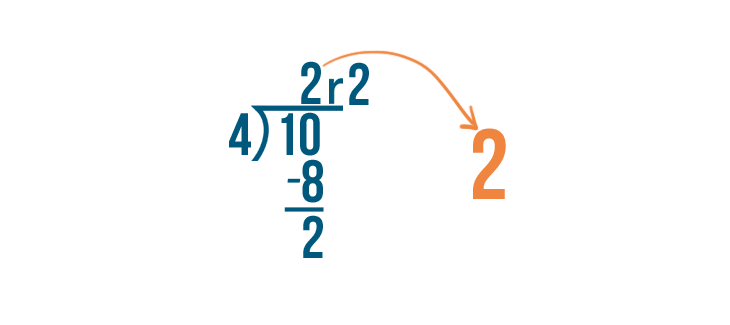
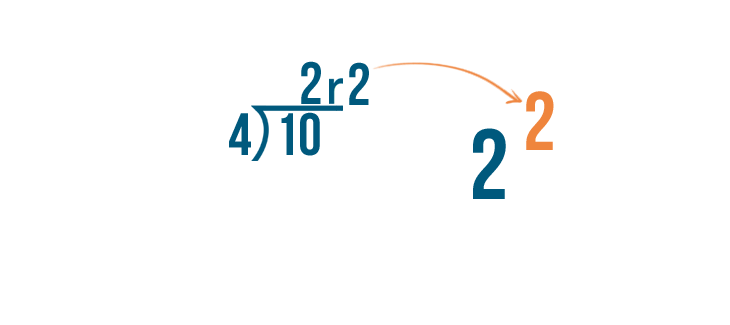
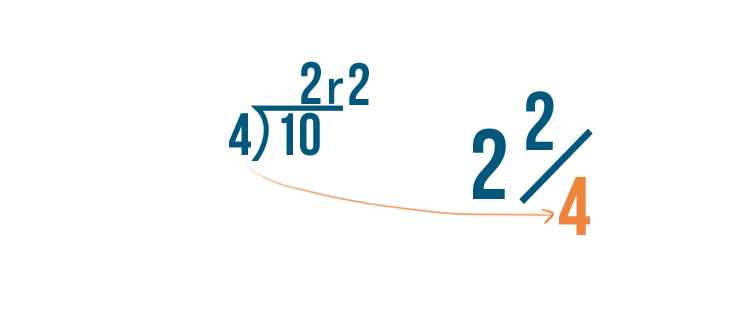
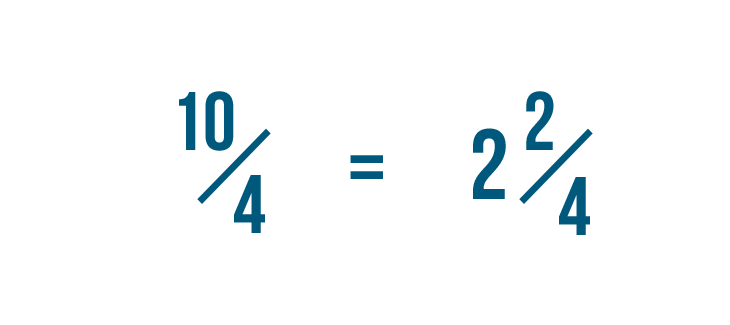
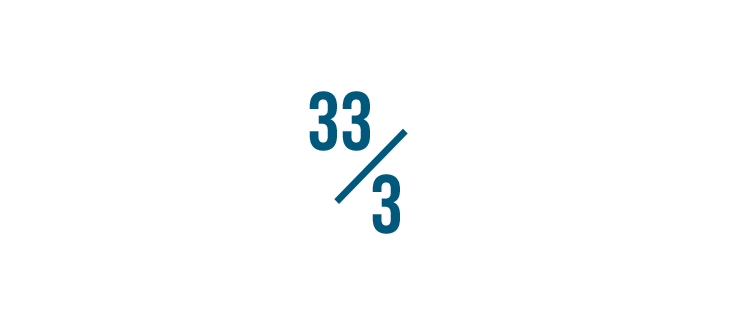
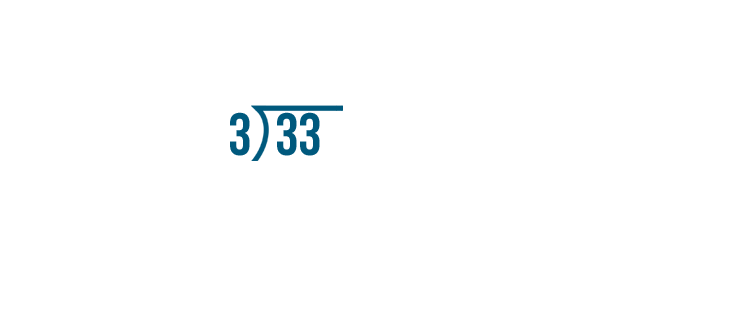
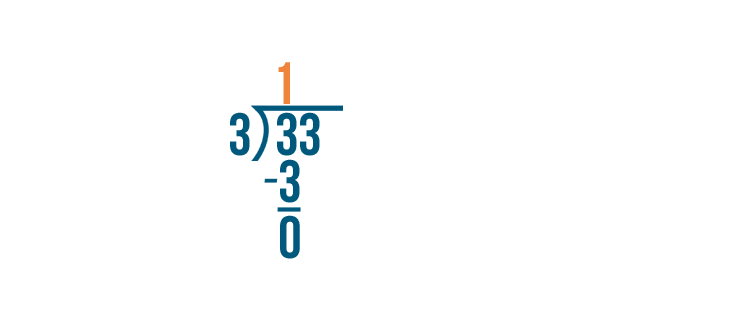
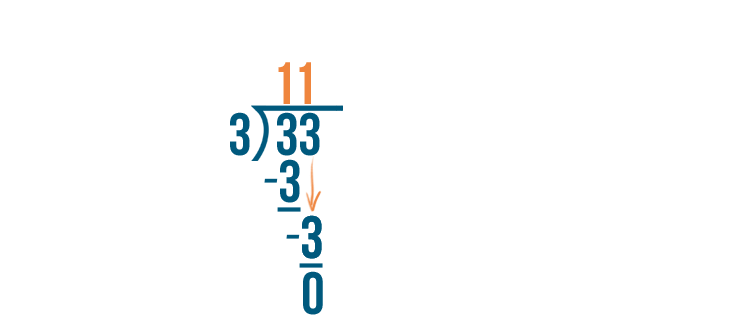
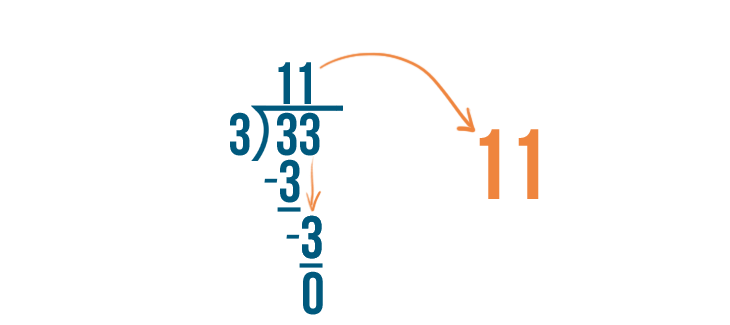
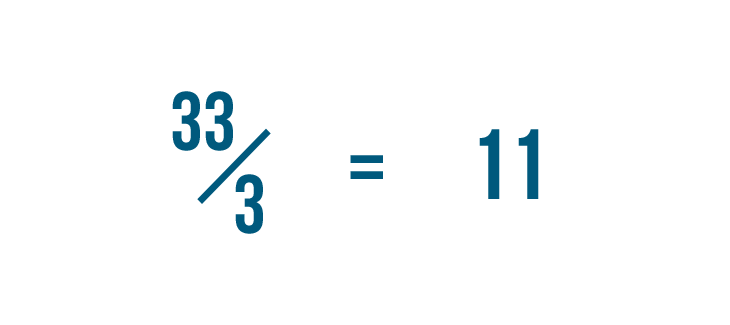

0 Response to "Is 5/4 Greater Than 1/2"
Post a Comment